dpadawer
Amorphous 3d Tapa
This is a Tapa variant:
Shade some blobs in 3d space. The grid is built of amorph blobs each containing one or more cells. A single blob must be either fully shaded or fully unshaded.
Numbered blobs may not be shaded.
We are going to differentiate “seeing” from “touching/contiguous”.
A cell sees the (up to) 26 cells around it that are at most 1 unit away in up to all 3 directions - that is, a cell can see the faces of a Rubik’s Cube if it were the core.
Two cells are touching/contiguous if they are separate by exactly one (given) line - that is, they are one apart in exactly one of their (x, y, z) coordinates and match in the other two.
A number on a blob tells how many sets of shaded regions there are that are contiguous within the seen cells of that region.
A 2x2x2 cube of cells may not be fully shaded.
All shaded blobs must form one contiguous region - again, contiguous means “there is a path along the given lines only taking a single step at a time”.
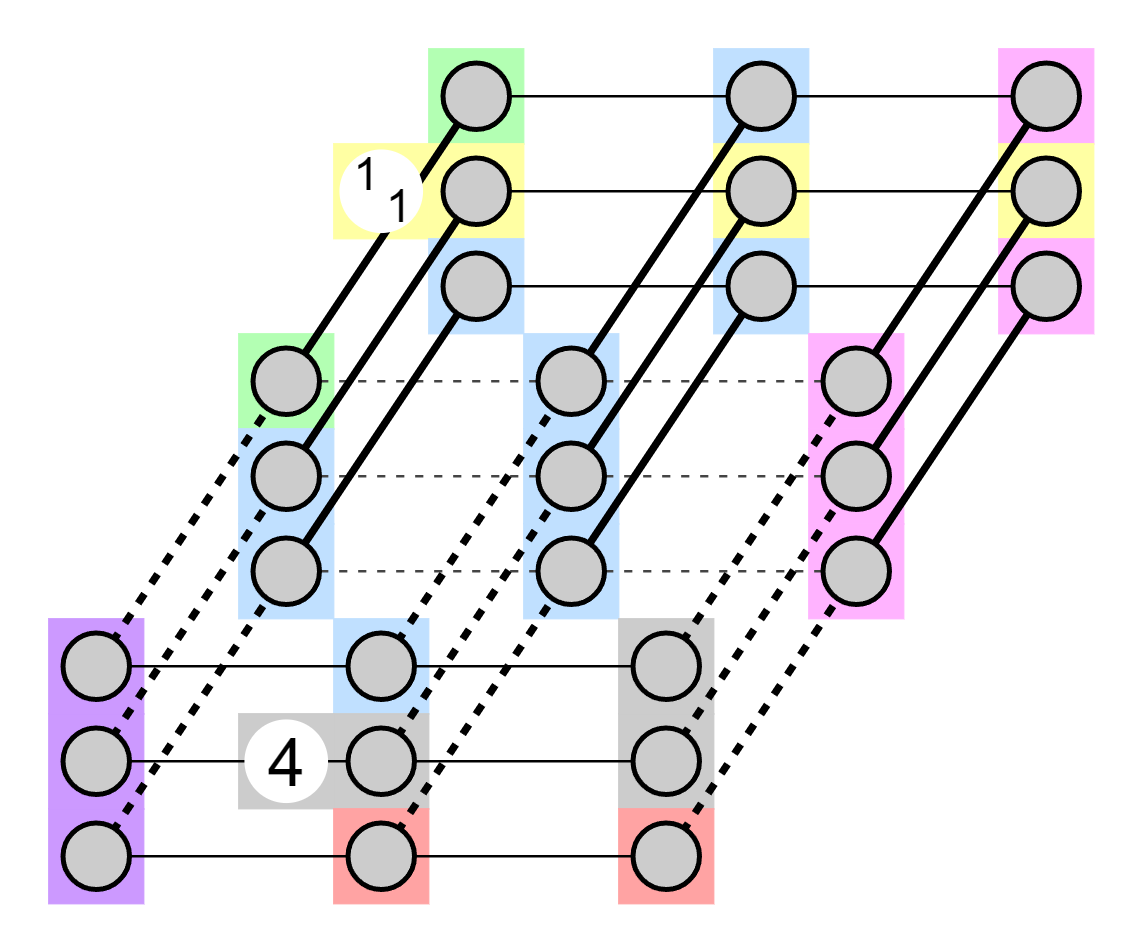
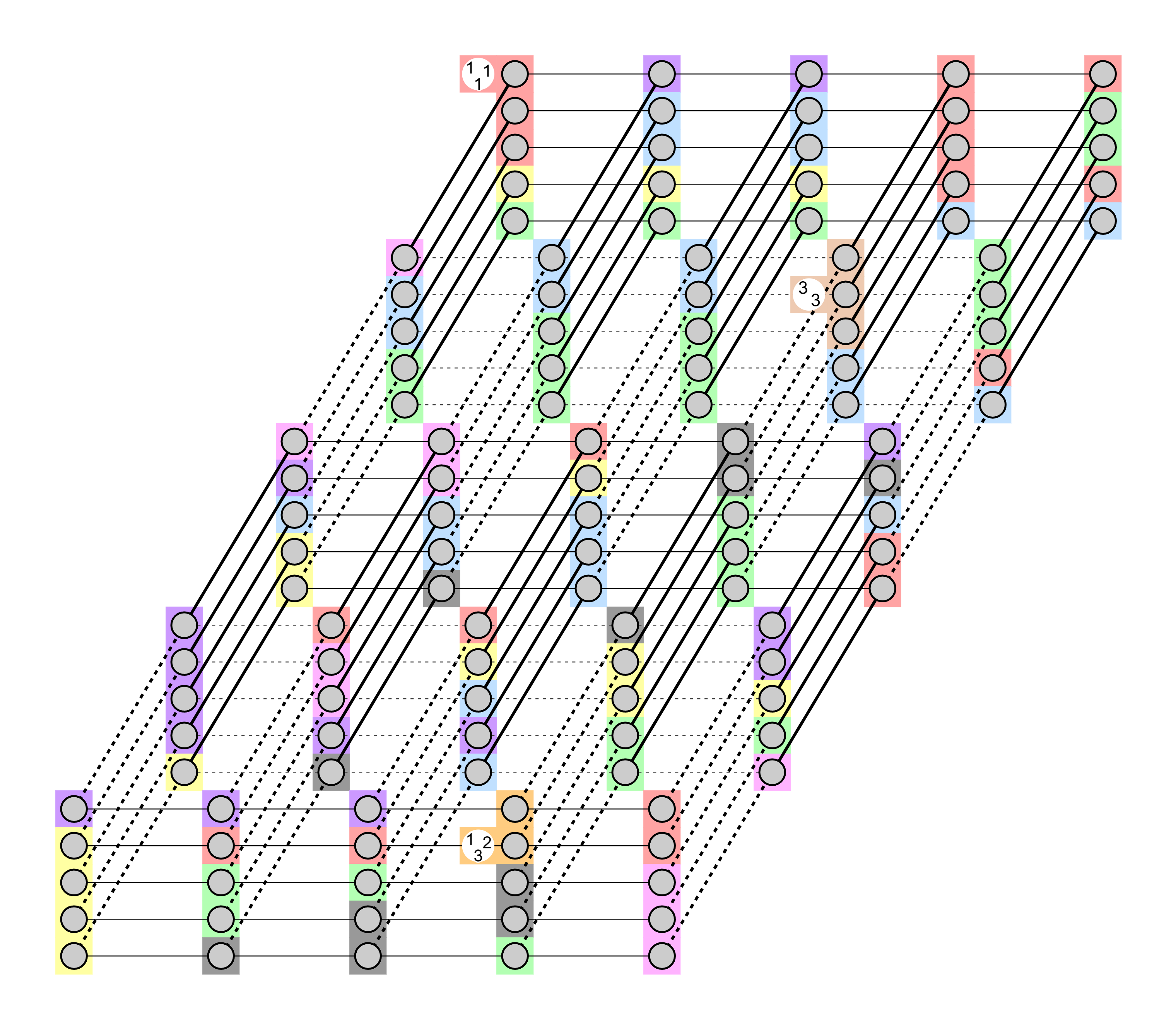
Two example puzzles with their solutions (click to solve on Penpa+):
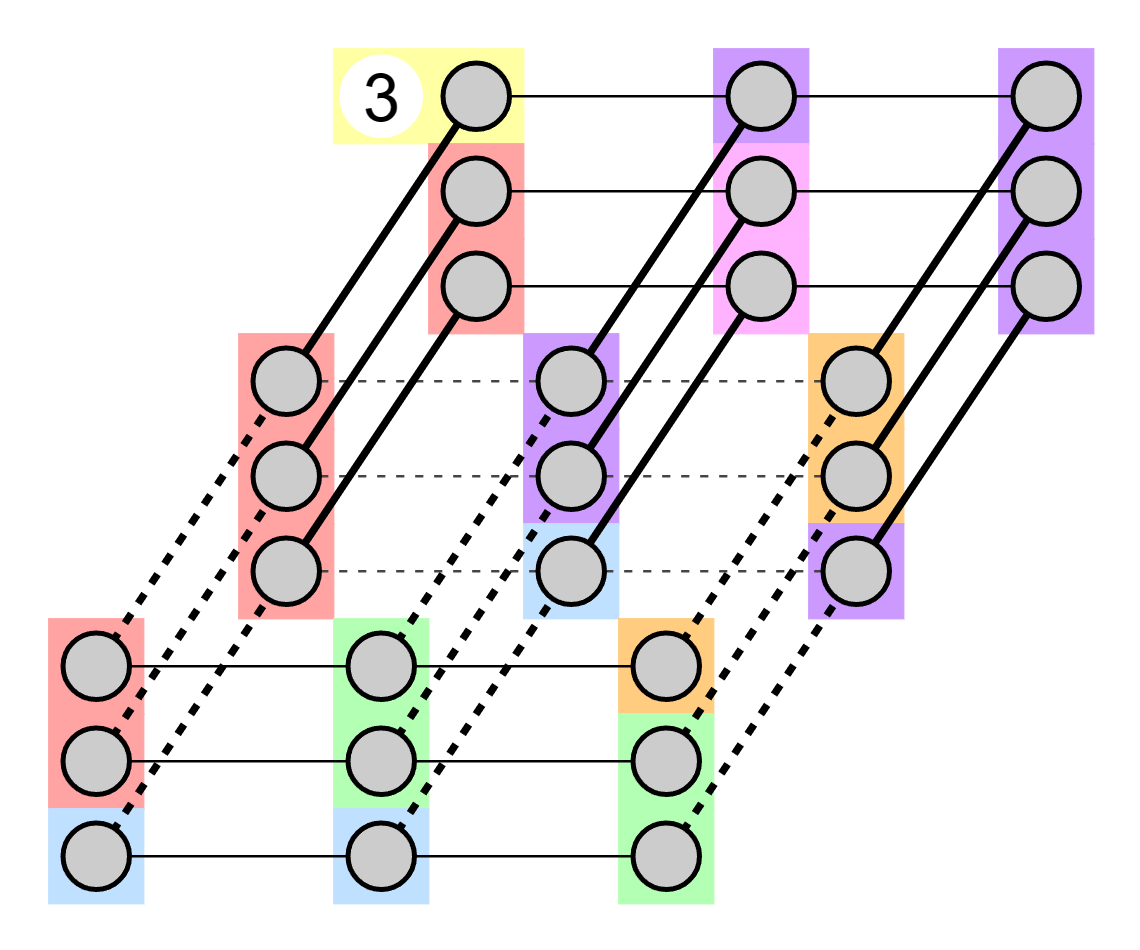Solution to example 1
Click the image to solve on Penpa+.
